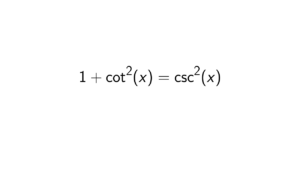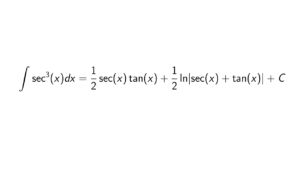How to show that every prime ideal in a P.I.D. is a maximal ideal
The easiest way to prove this is to use the definitions of a prime ideal, maximal ideal, and P.I.D. In the proof below, we want to show that P is either a maximal ideal or a P.I.D.
Prove that every prime ideal in P.I.D. is a maximal ideal
Proof: Let P = (p) and M = (m) be a prime ideal and a maximal ideal of the principal ideal domain R, respectively. Take for the assumption that P is contained in M. Then there exists an element r \in R such that p = rm. Since P is a prime ideal, we have that either r \in P or m \in P. If m \in P, then P is the maximal ideal. If r \in P, then r = px for some x \in R. Then p = rm = pxm which means that xm = 1, so this implies that m is a unit. So P = R.
Therefore, we have that P = M) or P = R).