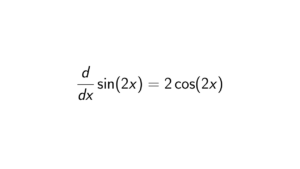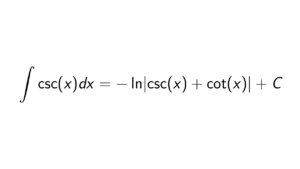How to prove that quotient of a principal ideal domain by a prime is again a P.I.D.

The best way to tackle this problem is by using the fact every prime ideal is a maximal ideal in a P.I.D.

Prove that a quotient of a P.I.D. by a prime ideal is again a P.I.D.

Proof: let P be a prime ideal of the principal ideal domain R. Every prime ideal is a maximal ideal in R, which we have proven here. So, we get that R/P is a field, again, which we have seen earlier here. Since R/P, it is definitely a P.I.D. too, which completes this proof.