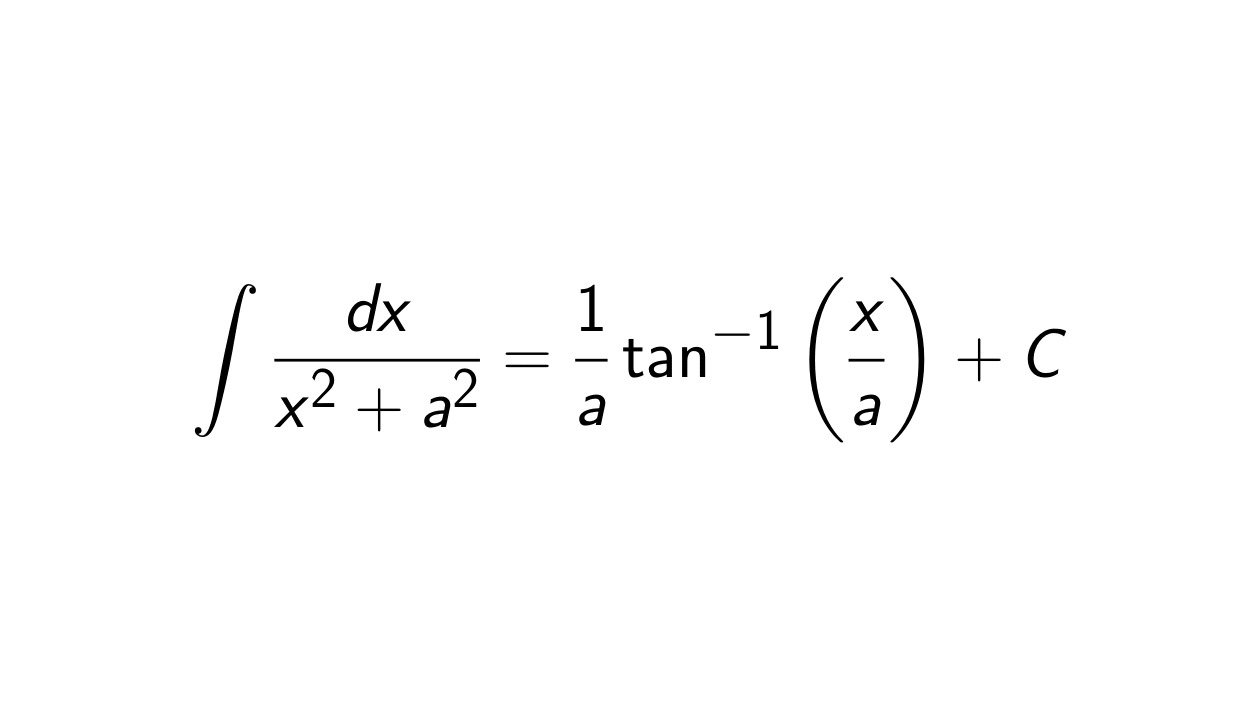What is the integral of 1/(x^2 + a^2)?
The integral of
\frac{1}{x^2 + a^2} is
\frac{1}{a}\tan^{-1}(\frac{x}{a}) + C.
Solution of the integral of 1/(x^2 + a^2)
Solution: While we could straightly use some integral techniques, the reader should remind itself that there is a function that if you take the derivative of that, then we get exactly the solution of
\frac{1}{x^2 + a^2}. Indeed, we get the following from
this article:
\begin{align*}
\frac{d}{dx} \frac{1}{a}\tan^{-1}\bigg(\frac{x}{a}\bigg) = \frac{1}{x^2 + a^2}.
\end{align*}
Now take the antiderivative of
\frac{1}{x^2 - a^2}, then we get that the integral of
\frac{1}{x^2 + a^2} is
\frac{1}{a}\tan^{-1}(\frac{x}{a}) + C.
Conclusion
Therefore, the integral of
\frac{1}{x^2 + a^2} is
\frac{1}{a}\tan^{-1}(\frac{x}{a}) + C, or in mathematical notation:
\begin{align*}
\int \frac{dx}{x^2 + a^2} = \frac{1}{a}\tan^{-1}\bigg(\frac{x}{a}\bigg) + C.
\end{align*}