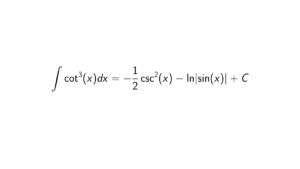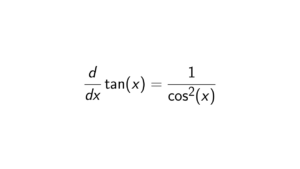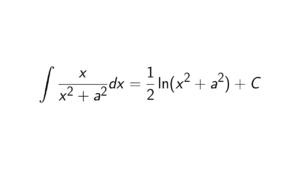Proof. In order to show that \text{im}(\phi) is a subgroup of H, it must hold the subgroup criterion. Firstly, we know that \text{im}(\phi) is nonempty since \phi(1_G) = 1_H, where 1_G and 1_H are identities of G and H, respectively. The easiest way to see that is that \phi(1_G) = \phi(1_G)\phi(1_G) = \phi(1_G)\phi(1_G), so it is getting cancelled. Secondly, let x,y \in \text{im}(\phi). We need to show that xy^{-1} \in \text{im}(\phi). Let a,b \in G such that \phi(a) = x and \phi(b) = y, and we know that ab^{-1} \in G. Then \phi(b)^{-1} = y^{-1}. So we get the following:
\begin{align*}
xy^{-1} &= \phi(a)\phi(b)^{-1} \\
&= \phi(a)\phi(b^{-1}) \\
&= \phi(ab^{-1}).
\end{align*}