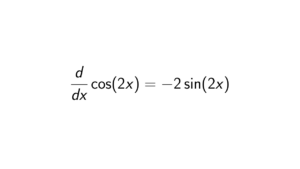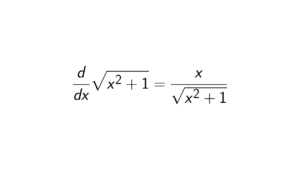Proof. Define
\begin{align*}
y = \lim_{x \rightarrow 0} (1 + x)^{\frac{1}{x}}
\end{align*}\begin{align*}
\ln(y) &= \ln\bigg(\lim_{x \rightarrow 0} (1 + x)^{\frac{1}{x}}\bigg) \\
&= \lim_{x \rightarrow 0} \ln\bigg[(1 + x)^{\frac{1}{x}}\bigg] \\
&= \lim_{x \rightarrow 0} \frac{\ln(1 + x)}{x},
\end{align*}\begin{align*}
\lim_{x \rightarrow 0} \frac{\ln(1 + x)}{x} = \frac{0}{0}.
\end{align*}\begin{align*}
\ln(y) &= \lim_{x \rightarrow 0} \frac{\frac{d}{dx}\ln(1 + x)}{\frac{d}{dx} x} \\
&= \lim_{x \rightarrow 0} \frac{\frac{1}{1+x}}{1} \\
&= \lim_{x \rightarrow 0} \frac{1}{1+x} \\
&= \frac{1}{1 + 0} \\
&= 1.
\end{align*}\begin{align*}
\ln(y) = 1 \iff e^{\ln(y)} = e^1 \iff y = e.
\end{align*}\begin{align*}
y = \lim_{x \rightarrow 0} (1 + x)^{\frac{1}{x}} = e.
\end{align*}