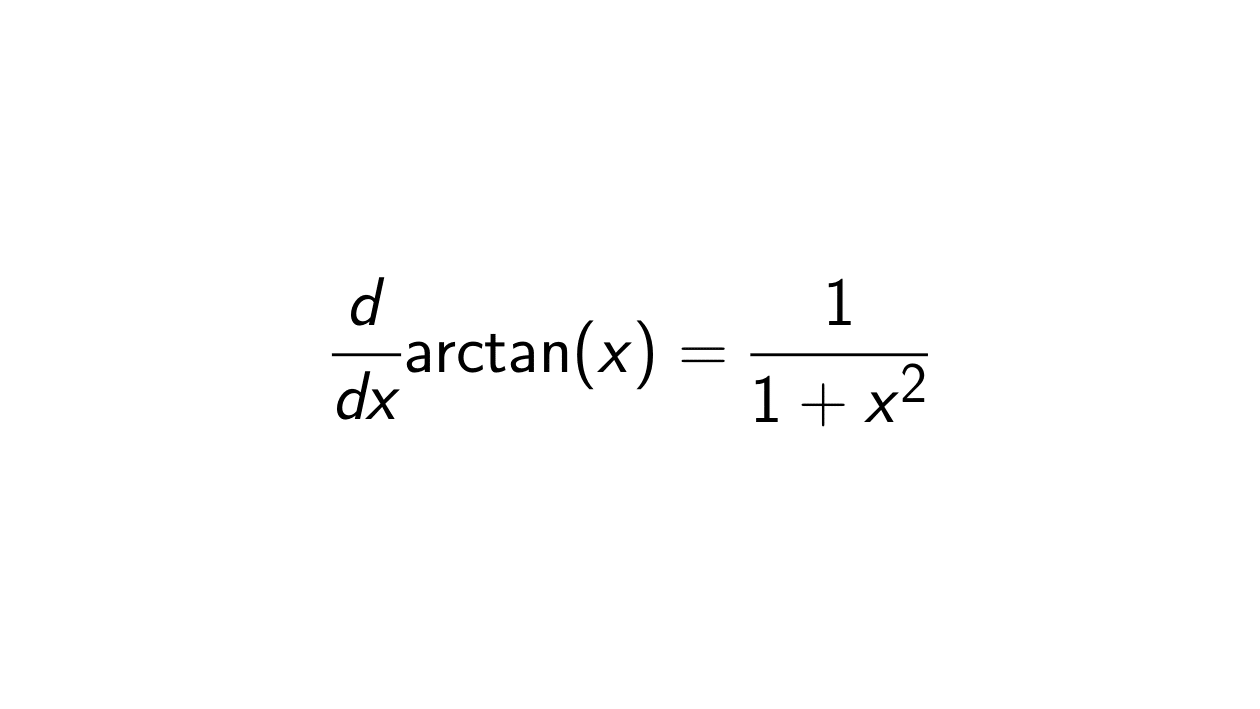What is the Derivative of arctan(x)?

Derivative of arctan(x)

The derivative of

\arctan(x)

\frac{1}{1 + x^2}

.

Proof. Let

y = \tan^{-1}(x)

. Then

x = \tan(y)

and

-\frac{\pi}{2}

y

\frac{\pi}{2 }

. We want to differentiate with respect to

x

, so we get:

\begin{align*} \frac{d}{dx} x = \frac{d}{dx} \tan(x) &\iff 1 = \frac{d(\tan(y))}{dy} \frac{dy}{dx} \\ &\iff 1 = \sec^2(y) \frac{dy}{dx} \\ &\iff \frac{dy}{dx} = \frac{1}{\sec^2(y)}, \end{align*}

where we have seen here that

\frac{d(\tan(y))}{dy} = \sec^2(y)

. We will apply the next identity:

\begin{align*} \sec^2(y) = 1 + \tan^2(y), \end{align*}

where we get that derivative of

\arctan(x)

is:

\begin{align*} \frac{d}{dx} \arctan(x) = \frac{d}{dx} \tan^{-1}(x) = \frac{dy}{dx} = \frac{1}{\sec^2(y)} = \frac{1}{1 + \tan^2(y)} = \frac{1}{1 + x^2}. \end{align*}

So, the derivative of

\arctan(x)

\frac{1}{1 + x^2}