Solution. Let f(x) = \frac{1}{x}. Then this can be rewritten as
\begin{align*}
f(x) = x^{-1}.
\end{align*}\begin{align*}
f'(x) = (-1) \cdot x^{-1 - 1} = -x^{-2}.
\end{align*}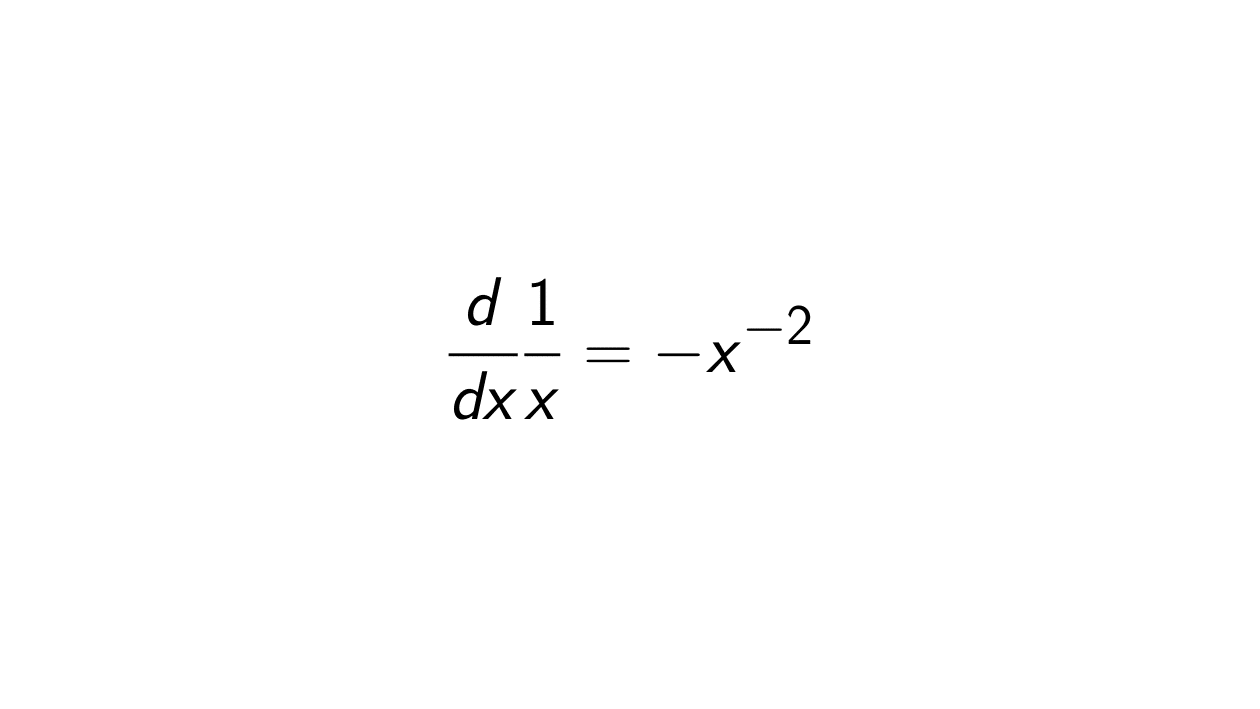
\begin{align*}
f(x) = x^{-1}.
\end{align*}\begin{align*}
f'(x) = (-1) \cdot x^{-1 - 1} = -x^{-2}.
\end{align*}