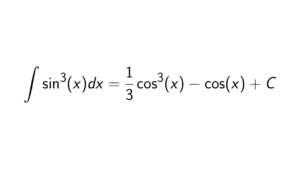How to prove that a Euclidean Domain has universal side divisors
The best way to prove that is to use the definition of a Euclidean Domain straightly and by using the definition of universal side divisors.
Prove that if R is a Euclidean domain and not a field, then there are universal side divisors in R
Proof: let
R be a Euclidean domain and let
b \in R - \widetilde{R} = R - R^{\times} \cup \{0\} be a universal side divisor of minimal norm. This means that we took a universal side divisor which we are sure that
R has no smaller norms of universal side divisors than the norm of
b. By the definition of the Euclidean Domain, we can say
\begin{align*}
x = qb + r \quad \text{where} \quad r = 0 \text{ or } N(r) < N(b).
\end{align*}
Now, we need to show that
r \in R^{\times} \cup \{0\}. It is obviously true that if
r = 0, then
r \in R^{\times} \cup \{0\}. If
N(r) <
N(b), then we do know that
r can't be a universal divisor since
b is the smallest norm that is a universal divisor, which implicates that
r \not \in R - \widetilde{R}. So
r must be a unit and therefore
r \in R^{\times} \cup \{0\}, which proves this proof.
Conclusion
It is crucial to notice that we are curious if
there are universal side divisors, so showing one is perfectly fine.