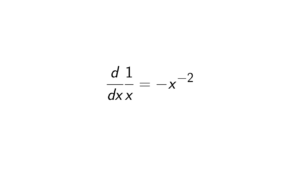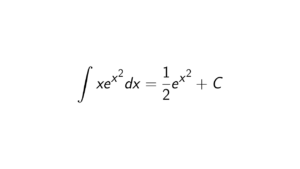Are the fields Euclidean domains?

The fields are Euclidean domains. To see why, we need to find a norm that satisfies the Division Algorithm.

Proof that the fields are Euclidean Domains

Let F be an arbitrary field. We can take the norm N(a) = 0 for all a \in F. Take a = qb + r. Since F is a field, each element has an inverse. Therefore, if we take r = 0 and q = ab^{-1} for every a and b \neq 0, we see that F possess a Division Algorithm. So, F is an Euclidean Domain.