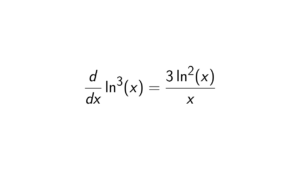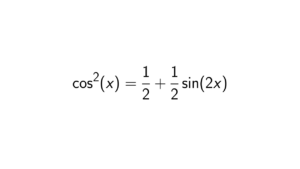In a Boolean ring every prime ideal is a maximal ideal

At first sight, it would not be easy to prove this by using the definitions of the prime ideal and maximal ideal itself. The trick is to use propositions that are for sure introduced earlier in any introduction book of ring theory.

Proof of that every prime ideal is a maximal ideal in a Boolean ring

Let P be a prime ideal of the Boolean ring R. Then R/P is a Boolean ring and an integral domain, which we have seen here. But we saw here that R \cong \mathbb{Z}/2\mathbb{Z}. Further, we do know that \mathbb{Z}/2\mathbb{Z} is a field, so is R since it is isomorphic to the integer modulo two. Now by this proposition, P is also a maximal ideal.

Conclusion

In a Boolean ring every prime ideal is a maximal ideal.