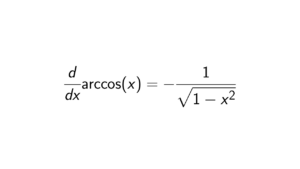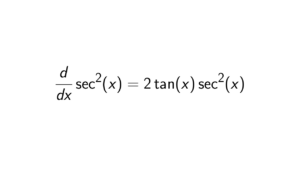I do expect that when you are learning group theory and you search for an answer to the question above, you want to know how to tackle such a question. While this can be answered in one sentence, I will take you through the whole process of what you need to do.
Proof. Let \mathbb{Z} be the set of integers. To be a group under multiplication, i.e., (\mathbb{Z},\times), we must verify three things: associativity, identity, and inverse elements. Let a,b,c \in \mathbb{Z}.
It is straightforward by the definition of integers that (a \times b)\times c = a \times (b \times c). So for all elements in \mathbb{Z} we know that the operation multiplication is associative.
Next, we need to find the identity element of \mathbb{Z} under multiplication. This is easy since 1 is identity element (note that a \times 1 = 1 \times a = a).
Finally, the last step is to find the inverse elements of \mathbb{Z} under multiplication. Now we take the element a \in \mathbb{Z}. Does this mean that there is an inverse element of a under multiplication? In other words, is there an element a^{-1} \in \mathbb{Z} such that:
\begin{align*}
a \times a^{-1} = a^{-1} \times a = 1?
\end{align*}A short counterexample you could give: 2 has no inverse element since \frac{1}{2} \not \in \mathbb{Z}.