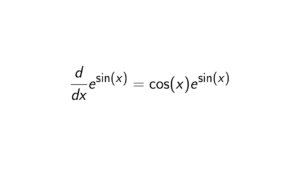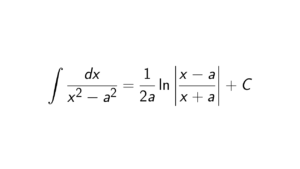What is a polynomial over GF(2)?
A polynomial of degree n over GF(2) is a polynomial f(x) = a_{0} + a_{1}x^{1} + \dots + a_{n}x^{n} with a_{0} \ldots a_{n} \in {0,1}. The set of all polynomials over GF(2) is denoted as GF(2)[x].Example. f(x) = 1 + x^2 where a_{0} = a_{2} = 1, and g(x) = 1 + x + x^2 where a_{0} = a_{1} = a_{2} = 1.
How to calculate f(x) mod g(x) over GF(2)
Now we are going to the point which you probably came for. How do we calculate f(x) modulo g(x)? We will give some examples.Example. Let f(x) = 1 + x + x^{7}, and g(x) = x^5. Then
\begin{equation*}
1 + x + x^7 \text{ mod } g(x) \equiv 1 + x + x^2
\end{equation*} Example. Let f(x) = 1 + x^4 + x^{5}, and g(x) = 1 + x + x^3. Then
\begin{align*}
1 + x^4 + x^5 \text{ mod } g(x) & \equiv 1 + x^3 x + x^3 x^2 \text{ mod } g(x) \\
& \equiv 1 + (1 + x) x + (1 + x) x^2 \text{ mod } g(x) \\
& \equiv 1 + x + x^2 + x^2 + x^3 \text{ mod } g(x) \\
& \equiv 1 + x + 2x^2 + (1 + x) \text{ mod } g(x) \\
& \equiv 0
\end{align*}