Blog

We will prove that the limit of \sin(x)/x as x approaches 0 is equal to 1. We will prove that via the squeeze theorem.

This is also crucial to understand if someone has never seen concepts like l’ Hopital or Maclaurin series.

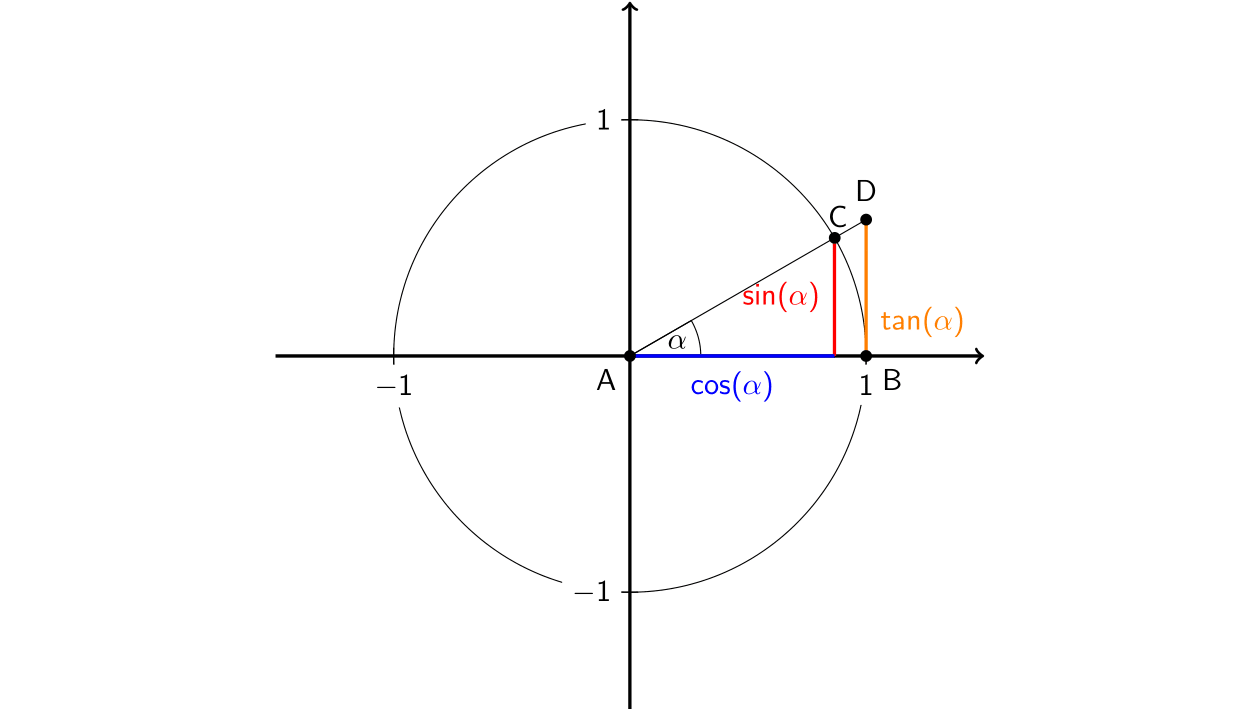
Proof. We will recall the definitions of the trigonometric functions with the definitions opposite, hypotenuse, and adjacent:

\begin{equation*}
\sin(\alpha) = \frac{\text{opp}}{\text{hyp}}, \ \cos(\alpha) = \frac{\text{adj}}{\text{hyp}}, \ \text{and} \tan(\alpha) = \frac{\text{opp}}{\text{adj}} 
\end{equation*}

We want to determine the areas in the above unit circle on the interval (0, \pi/2). The triangle area \triangle ABC is equal to \sin(\alpha)/2 because hyp = 1. The circular sector ⌔ ABC is equal to \frac{1}{2}r\alpha = \frac{1}{2}\alpha because the radius r is equal to 1. The last triangle area \triangle ACD is equal to \tan(\alpha)/2 because adj = 1. Therefore we get the next inequality:

\begin{align*}
\frac{\sin(\alpha)}{2} < \frac{\alpha}{2} < \frac{\tan(\alpha)}{2}.
\end{align*}

The first question might pop up: why do we have strict inequalities while the squeeze theorem explicitly states it needs to be "\leq"? The reason that for that is if we take x \leq y, then x < y OR x = y. So we can use strict inequalities for the squeeze theorem. Now we will divide all the functions with \frac{\sin(\alpha)}{2} and taking the fact that \tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)}:

\begin{align*}
1 < \frac{\alpha}{\sin(\alpha)} < \frac{1}{\cos(\alpha)}.
\end{align*}

Now taking the reciprocals, which means inversing the functions:

\begin{align*}
\cos(\alpha) < \frac{\sin(\alpha)}{\alpha} < 1.
\end{align*}

Now we have that

\begin{align*}
\lim_{\alpha \rightarrow 0} \cos(\alpha) = 1 \ \text{and} \ \lim_{\alpha \rightarrow 0} 1 = 1
\end{align*}

Therefore, by the squeeze theorem, we get

\begin{align*}
1 = \lim_{\alpha \rightarrow 0} \cos(\alpha) = \lim_{\alpha \rightarrow 0} \frac{\sin(\alpha)}{\alpha} = \lim_{\alpha \rightarrow 0} 1 = 1
\end{align*}

This implies that \lim_{\alpha \rightarrow 0} \frac{\sin(\alpha)}{\alpha} = 1, which proves this proof.

There are also two other ways to prove that \lim_{\alpha \rightarrow 0} \frac{\sin(\alpha)}{\alpha}, but that is also a circular reasoning:

Proof. The easiest way is to apply l' Hopital, and we can apply that here because we do have that

\begin{equation*}
\lim_{x \rightarrow 0} \frac{\sin(x)}{x} = \frac{0}{0}.
\end{equation*}

Therefore, we get

\begin{align*}
\lim_{x \rightarrow 0} \frac{\sin(x)}{x} &= \lim_{x \rightarrow 0} \frac{\frac{d}{dx}\sin(x)}{\frac{d}{dx}x} \\
&= \lim_{x \rightarrow 0} \frac{\cos(x)}{1} \\
&= \cos(0)\\
&= 1,
\end{align*}

since we have proved that the derivative of \sin(x) is \cos(x) here. The first approach is straightforward. The second way is more beautiful, as we will use Maclaurin series. Note that

\begin{align*}
\sin(x) &= \sum_{n = 0}^{\infty} \frac{(-1)^n}{(2n + 1)!} x^{2n + 1} \\
&= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots
\end{align*}

We will substitute that in the limit:

\begin{align*}
\lim_{x \rightarrow 0} \frac{\sin(x)}{x} &= \lim_{x \rightarrow 0} \frac{\sum_{n = 0}^{\infty} \frac{(-1)^n}{(2n + 1)!} x^{2n + 1}}{x} \\
&= \lim_{x \rightarrow 0}\frac{1}{x}(x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots) \\
&= \lim_{x \rightarrow 0} 1 - \frac{x^2}{3!} + \frac{x^4}{5!} - \cdots \\
&= 1 - 0 + 0 - \cdots \\
&= 1
\end{align*}

which completes the proofs.