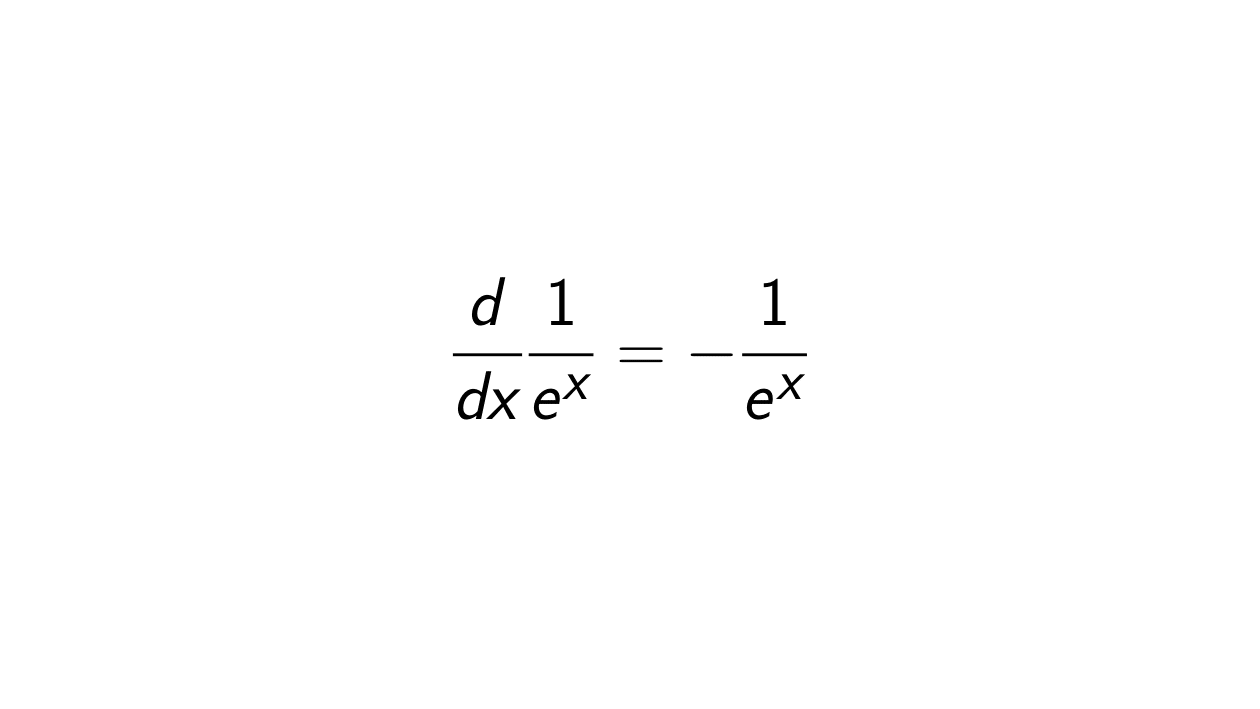Solution. Let h(x) = \frac{1}{e^x} = e^{-x}, f(u) = e^u and g(x) = -x. We will use the chain rule, i.e.,
\begin{align*}
h'(x) = f'(g(x))g'(x).
\end{align*}\begin{align*}
f(u) = e^u \quad \text{and} \quad g(x) = -1.
\end{align*}\begin{align*}
h'(x) &= f'(g(x))g'(x) \\
&= e^{-x} \cdot (-1) \\
&= -e^{-x} \\
&= -\frac{1}{e^{-x}}
\end{align*}