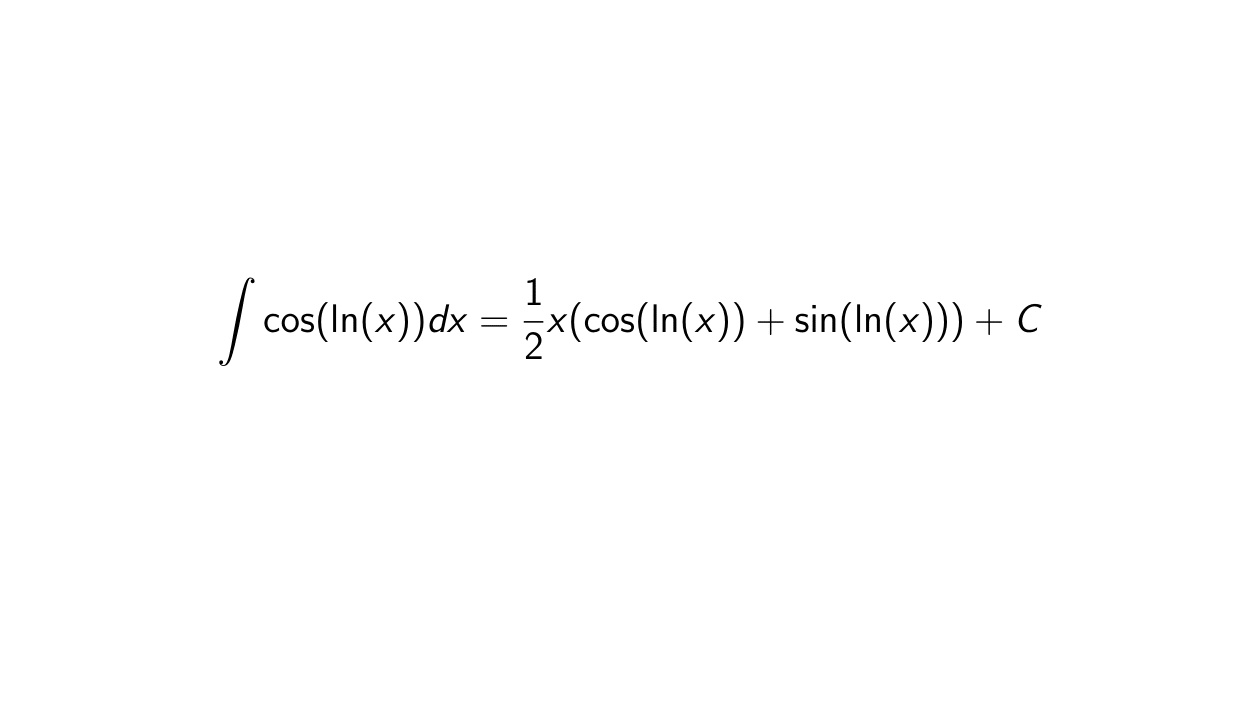What is the integral of cos(ln(x))?

The integral of

\cos(\ln(x))

\frac{1}{2}x(\cos(\ln(x)) + \sin(\ln(x))) + C

.

Solution. We need to find out what the integral of

\cos(\ln(x))

is, that is:

\begin{align*} I = \int \cos(\ln(x)) dx. \end{align*}

We will apply integration by parts with the following formula:

\begin{align*} \int UdV = UV - \int VdU. \end{align*}

By applying the integration by parts, we will consider the following formulas:

\begin{align*} U = \cos(\ln(x)), \quad &dV = dx\\ dU = \frac{-\sin(\ln(x))}{x}dx, \quad &V = x. \end{align*}

The derivative of

U

, which we see above, can be verified here. So we get the following integral:

\begin{align*} \int \cos(\ln(x)) dx = x\cos(\ln(x)) + \int \sin(\ln(x))dx. \end{align*}

Secondly, we integrate by parts again for

\int \sin(\ln(x))dx

\begin{align*} U = \sin(\ln(x)), \quad &dV = dx\\ dU = \frac{\cos(\ln(x))}{x}dx, \quad &V = x. \end{align*}

To see how we did

dU

, see here. Therefore, combined with the previous integral, we get:

\begin{align*} \int \cos(\ln(x)) dx &= x\sin(\ln(x)) + \int \sin(\ln(x))dx \\ &= x\cos(\ln(x)) + x\sin(\ln(x)) - \int \cos(\ln(x))dx \\ &= x\cos(\ln(x)) + x\sin(\ln(x)) - I. \end{align*}

Now we bring

I

to the left-hand side and divide by 2. So we finally get the integral we wanted:

\begin{align*} \int \cos(\ln(x)) dx = \frac{1}{2}x(\cos(\ln(x)) + \sin(\ln(x))) + C. \end{align*}

Therefore, the integral of

\sin(\ln(x))

\frac{1}{2}x(\cos(\ln(x)) + \sin(\ln(x))) + C