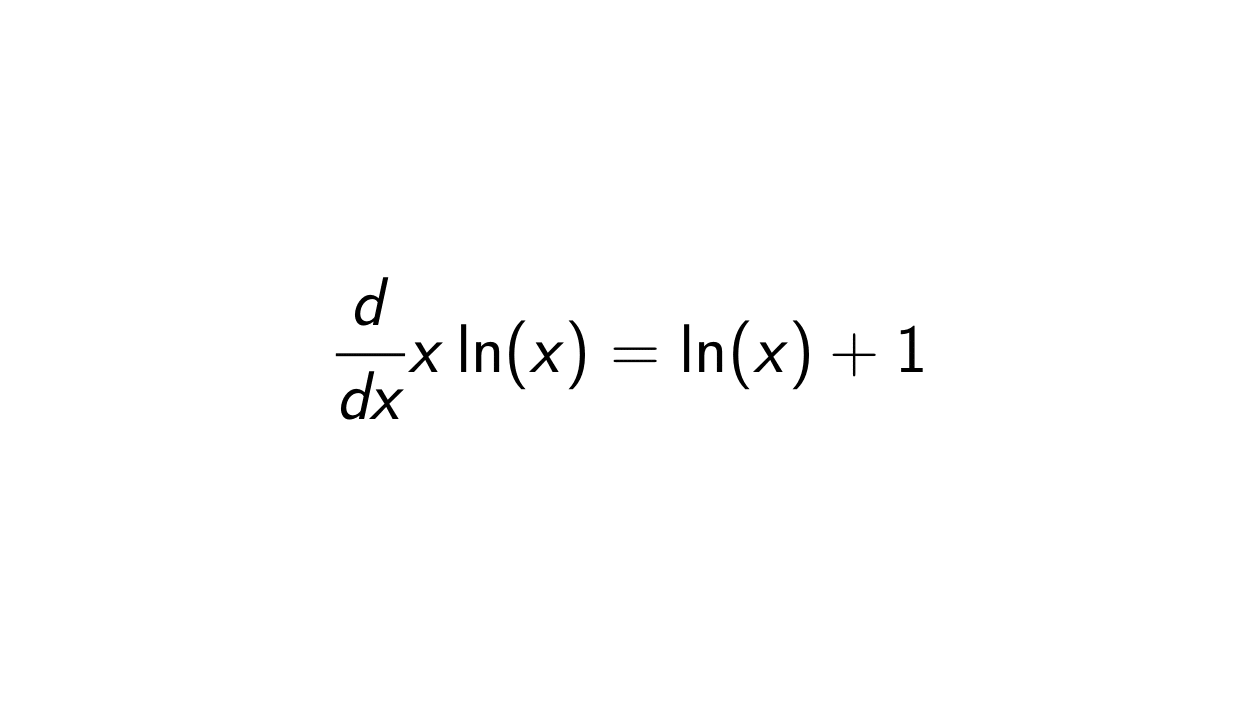What is the Derivative of xln(x)?

derivative of xln(x)

What is the derivative of xln(x)?

The derivative of

x\ln(x)

\ln(x) + 1

.

Proof. Let

f(x) = x

and

g(x) = \ln(x)

. We will use the product rule:

\begin{align*} (f(x)g(x))' = f'(x)g(x) + f(x)g'(x). \end{align*}

This would mean that

\begin{align*} f'(x) = 1, \end{align*}

and

\begin{align*} g'(x) = \frac{1}{x} \end{align*}

as we have shown here. Wrapping everything together, we get

\begin{align*} (f(x)g(x))' &= f'(x)g(x) + f(x)g'(x) \\ &= 1\cdot \ln(x) + x\frac{1}{x}\\ &= \ln(x) + 1. \end{align*}

Therefore, we have that the derivative of

x\ln(x)

\ln(x) + 1