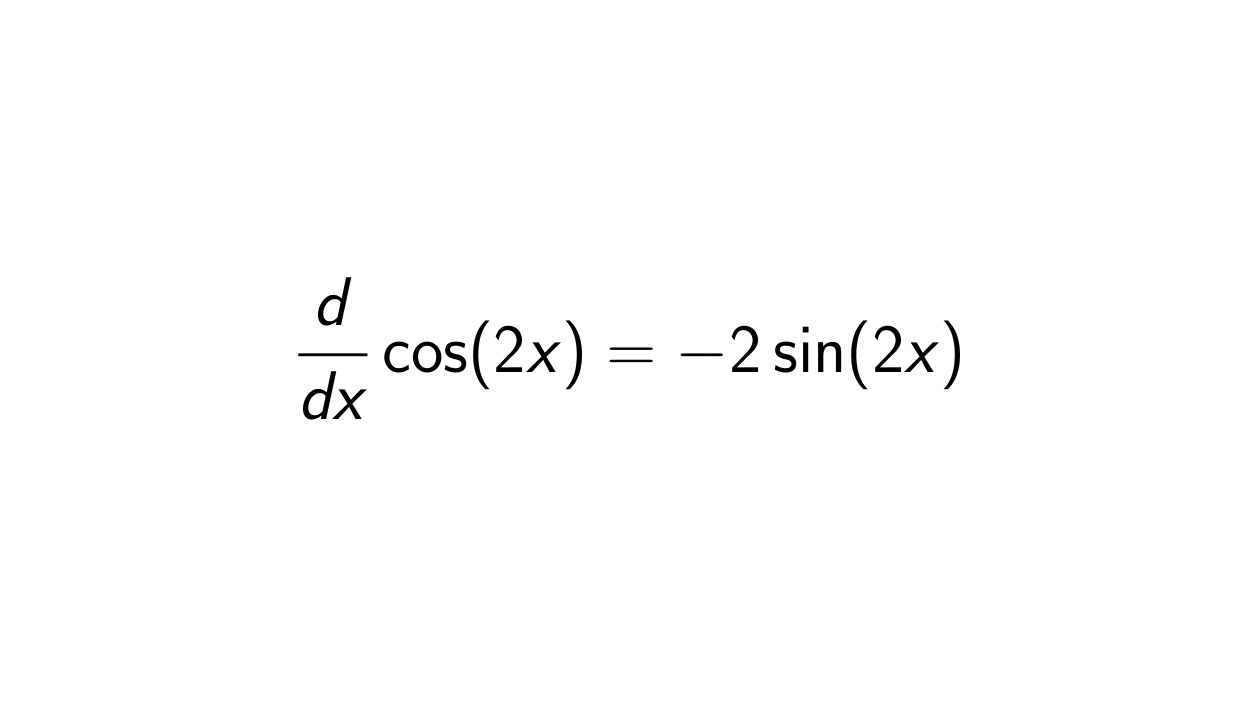What is the derivative of cos(2x)?

derivative of cos(2x)

We will determine the derivative of

\cos(2x)

.

Proof. Let

F(x) = \cos(2x)

f(u) = \cos(u)

, and

g(x) = 2x

such that

F(x) = f(g(x))

. To prove the derivative of

\cos(2x)

, we will use the chain rule:

\begin{align*} F'(x) = f'(g(x))g'(x). \end{align*}

We have seen here that

f'(u) = \frac{d}{du} \cos(u) = -\sin(u)

, and

\frac{d}{dx} 2x = 2

. Therefore, we get

\begin{align*} f'(g(x)) = -\sin(g(x)) = \sin(2x) \quad \text{ and } \quad g'(x) = 2. \end{align*}

Substituting everything together, we get

\begin{align*} F'(x) &= f'(g(x))g'(x) \\ &= -\sin(2x)\cdot 2 \\ &= -2\sin(2x). \end{align*}

Therefore, we see that the derivative of

\cos(2x)

-\sin(2x)