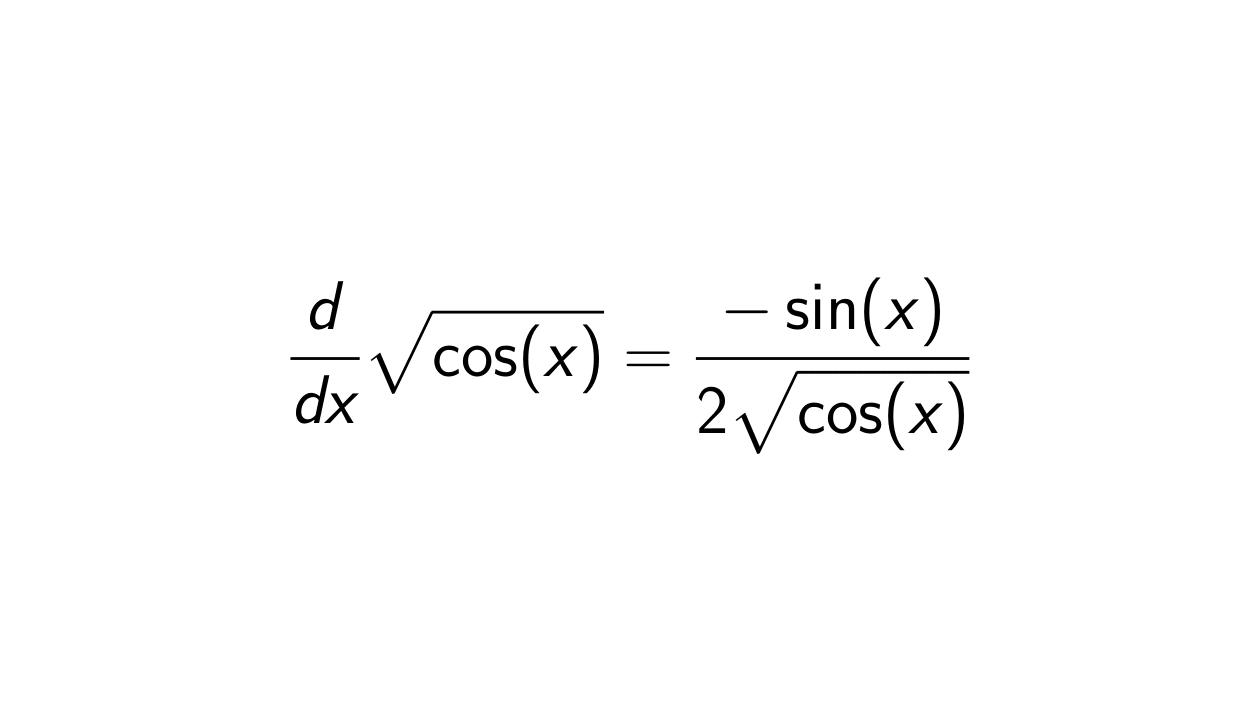What is the derivative of square root cos(x)?
The derivative of square root
\cos(x) is
\frac{-\sin(x)}{2\sqrt{\cos(x)}}.
Solution of the derivative of square root cos(x)
Let
F(x) = f(g(x)) = \sqrt{\cos(x)}, where
f(u) = \sqrt{u} and
g(x) = \cos(x). To find the derivative of
\sqrt{\cos(x)}, we need to apply the chain rule:
\begin{align*}
F'(x) = f'(g(x))g'(x).
\end{align*}
We know from
here that
f'(u) = \frac{1}{2\sqrt{u}} and
here that
g'(x) = -\sin(x). Therefore, we get:
\begin{align*}
f'(g(x)) = \frac{1}{2\sqrt{g(x)}} = \frac{1}{2\sqrt{\cos(x)}} \quad \text{and} \quad g'(x) = -\sin(x).
\end{align*}
Finally, this gives us the desired result:
\begin{align*}
F'(x) &= f'(g(x))g'(x) \\
&= \frac{1}{2\sqrt{g(x)}} \cdot (-\sin(x)) \\
&= \frac{-\sin(x)}{2\sqrt{\cos(x)}}.
\end{align*}Conclusion
Therefore, the derivative of square root
\sqrt{\cos(x)} is
\frac{-\sin(x)}{2\sqrt{\cos(x)}}.