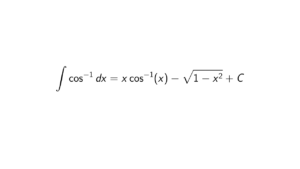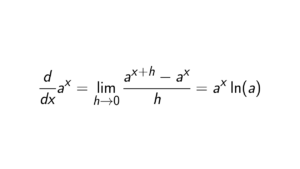By definition, a ring R is Boolean if x^2 = x, \forall x \in R.
Proof. We need to show that xy = yx for all x,y \in R. So first, we have:
\begin{align*}
(x + y)^2 = (x + y) &\iff x^2 + xy + yx + y^2 = x + y \\
&\iff x + xy + yx + y = x + y \\
&\iff xy + yx = 0
\end{align*}\begin{align*}
(y + y) &= (y + y)^2 \\
&= y^2 + 2y + y^2 \\
&= y + y + y + y \\
&= 0
\end{align*}