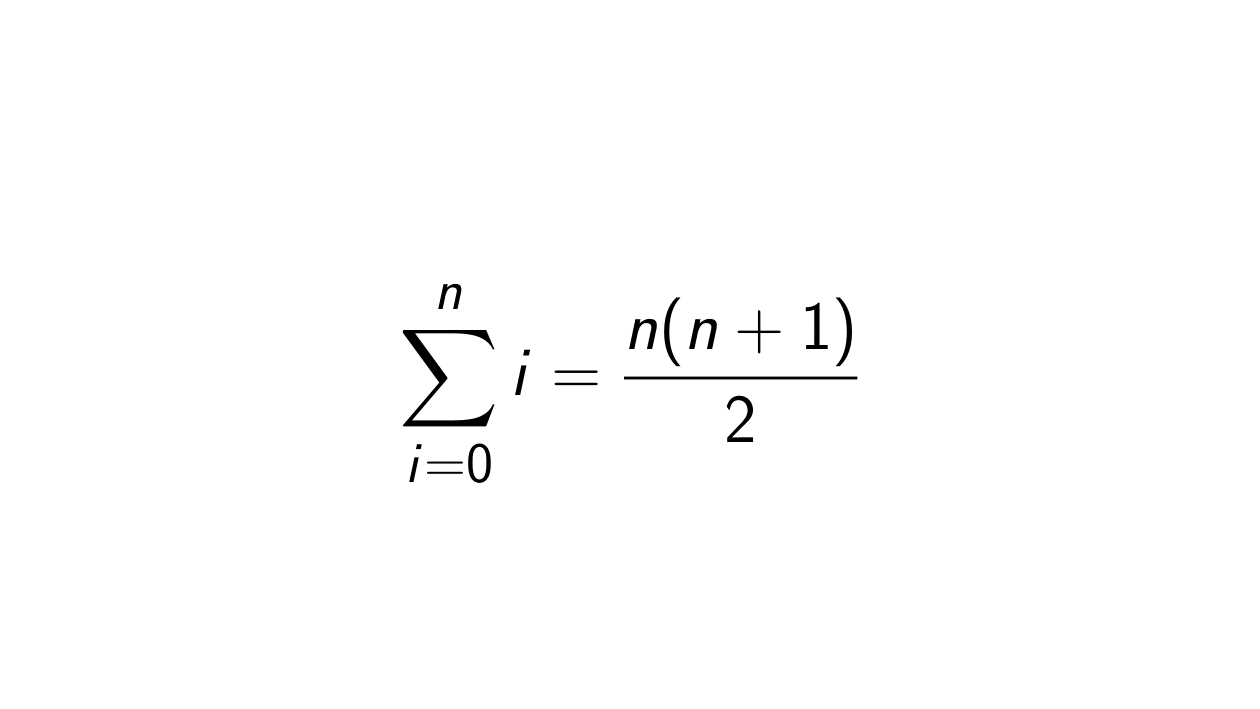Blog

You are currently viewing The Finite Sum Of Natural Numbers
Finite sum of natural numbers

The Finite Sum Of Natural Numbers

In this article, we will prove the finite sum of natural numbers via the direct way and induction. We have the following sum, which is the finite sum of natural numbers 
\begin{equation*}
\sum_{i = 0}^n i = \frac{n(n+1)}{2}
\end{equation*}
Proof 1. We start with induction. For the base case, if n = 0, then 
\begin{equation*}
\sum_{i = 0}^0 i = 0 = \frac{0(0+1)}{2} = 0
\end{equation*}
which holds. For the induction step, we take for the induction hypothesis that the sum holds for n, and we want to show that it holds too for n + 1. So summing up to and including n + 1, we get 
\begin{align*}
\sum_{i = 0}^{n+1} i &= \frac{(n + 1)((n + 1) +1)}{2} \\ 
&= \frac{n(n+1) + 2n + 2}{2} \\
&= \frac{n(n+1)}{2} + \frac{2n + 2}{2} \\
&= \frac{n(n+1)}{2} + (n + 1) \\
&= (\sum_{i = 0}^{n} i) + (n + 1) = \sum_{i = 0}^{n + 1} i
\end{align*}
which proves that the summation is correct.

Proof 2. Another way to prove it is to reverse the sum from n to 0, i.e., 
\begin{align*}
n + (n-1) + \cdots + 2 + 1 
\end{align*}
Now we take the sum which we have seen earlier and the reverse version: 
\begin{alignat*}{4}
1 &+ 2 &&+ \cdots &&+ (n - 1) &&+ n \\
n &+ (n-1) &&+ \cdots &&+ 2 &&+ 1\\ 
\end{alignat*}
We will sum the two sums above: n + 1 = n + 1, (n - 1) + 2 = n + 1, \ldots, 1 + n = n + 1. This happens n times. So we get 
\begin{equation*}
2 \cdot \sum_{i = 0}^n i = n(n + 1)
\end{equation*}
Now divide out 2 on both sides, and we get 
\begin{equation*}
\sum_{i = 0}^n i = \frac{n(n+1)}{2}
\end{equation*}
which finishes the proof.
Tags: ,

Leave a Reply