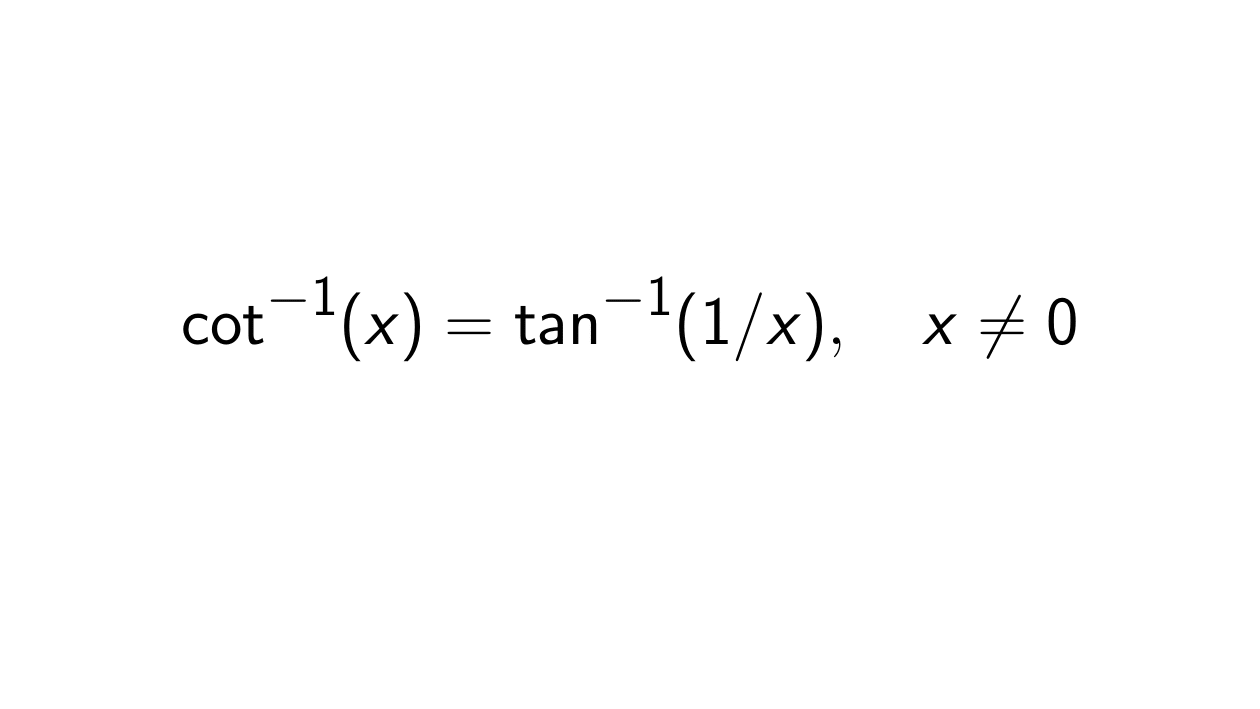Prove that cot^-1(x) is equal to tan^-1(1/x)

arccot(x) is equal to arctan(1/x)

The function

\cot^{-1}(x)

is equal to

\tan^{-1}(1/x)

for

x \neq 0

.

Proof. Take the following functions into account:

\begin{align*} \cot^{-1}(x), \text{ where } x \neq 0, \end{align*}

and

\begin{align*} \tan^{-1}(x), \text{ where } x \text{ is defined everywhere.} \end{align*}

Let

y = \cot^{-1}(x)

. Then:

\begin{align*} y = \cot^{-1}(x) &\iff \cot(y) = x \\ &\iff \frac{1}{\tan(y)} = x \\ &\iff y = \tan^{-1}(1/x), \end{align*}

where

\cot(y) = \frac{1}{\tan(y)}

by definition. Since

y = \cot^{-1}(x)

, we get that

\cot^{-1}(x) = \tan^{-1}(1/x)

for

x \neq 0

. So,

\cot^{-1}(x)

is equal to

\tan^{-1}(1/x)

for

x \neq 0